Математики пытаются решить старую головоломку и разрезать бесконечный блин на как можно больше частей

Ко­ман­да ма­те­ма­ти­ков из США пы­та­ет­ся раз­ре­зать бес­ко­неч­ный блин на мак­си­маль­ное чис­ло кус­ков. Уче­ные пред­ла­га­ют ре­шать эту го­ло­во­лом­ку не толь­ко с по­мо­щью пря­мо­го ножа, но и ряда но­жей при­чуд­ли­вой фор­мы. Их еще неопуб­ли­ко­ван­ное ис­сле­до­ва­ние на­зы­ва­ет­ся «Раз­ре­за­ние бли­на эк­зо­ти­че­ским но­жом». Об этом со­об­ща­ет The New York Times.

На пер­вый взгляд за­да­ча ка­жет­ся про­стой, но ее об­суж­да­ют уже несколь­ко де­ся­ти­ле­тий. Этот блин бес­ко­не­чен, он бес­ко­неч­но рас­те­ка­ет­ся во всех на­прав­ле­ни­ях.

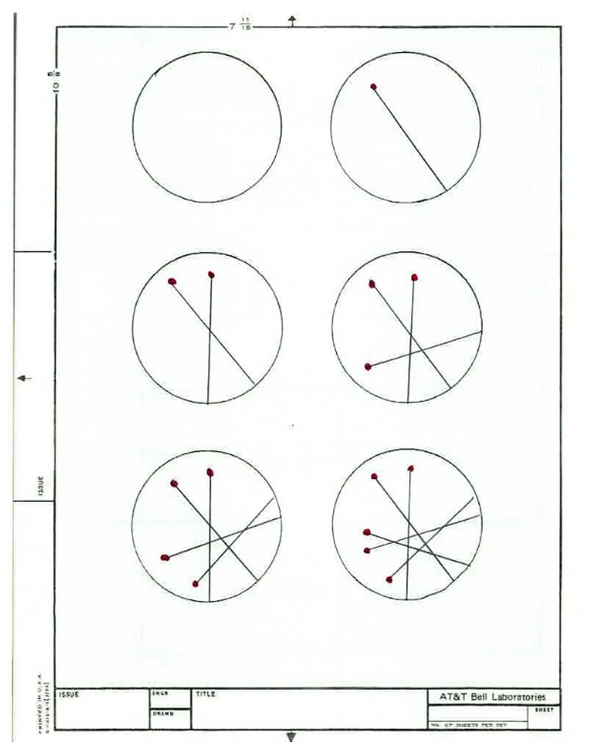
«Об­щая фи­ло­со­фия за­клю­ча­ет­ся в том, что при вы­пол­не­нии раз­ре­за необ­хо­ди­мо по­пы­тать­ся пе­ре­сечь все преды­ду­щие ли­нии», — за­явил про­фес­сор, со­зда­тель он­лай­но­вой Эн­цик­ло­пе­дии це­ло­чис­лен­ных по­сле­до­ва­тель­но­стей и ав­тор ис­сле­до­ва­ния Нил Джеймс Алек­сандр Сло­ун.

Ножи, ис­поль­зо­ван­ные док­то­ром Сло­уном и сту­ден­том Тафт­ско­го уни­вер­си­те­та Дэ­ви­дом Кат­ле­ром, были со­гну­ты в неесте­ствен­ные фор­мы. И с по­мо­щью этих эк­зо­ти­че­ских но­жей, по сло­вам Сло­у­на, лю­бые вы­сту­па­ю­щие «руки или ноги» (кон­цы но­жей) ста­но­вят­ся бес­ко­неч­но длин­ны­ми.

На­при­мер, один из мно­гих пред­ло­жен­ных ре­жу­щих ин­стру­мен­тов имел фор­му ле­ден­ца на па­лоч­ке с бес­ко­неч­ной нож­кой. Дру­гой пред­став­лял со­бой за­глав­ную бук­ву «А», у ко­то­рой по­пе­реч­ная пе­ре­кла­ди­на была за­креп­ле­на го­ри­зон­таль­но та­ким об­ра­зом, что вме­сте с кон­чи­ком бук­вы «А» она об­ра­зо­вы­ва­ла ос­но­ва­ние рав­но­бед­рен­но­го тре­уголь­ни­ка.

Для ре­ше­ния го­ло­во­лом­ки уче­ные со­зда­ли спе­ци­аль­ную ком­пью­тер­ную про­грам­му, ко­то­рая счи­та­ет, на сколь­ко ча­стей раз­ные ножи де­лят блин. Без ком­пью­те­ра ре­шить за­да­чу слож­но, так как на бу­ма­ге недо­ста­точ­но ме­ста для бес­ко­неч­но­го бли­на.

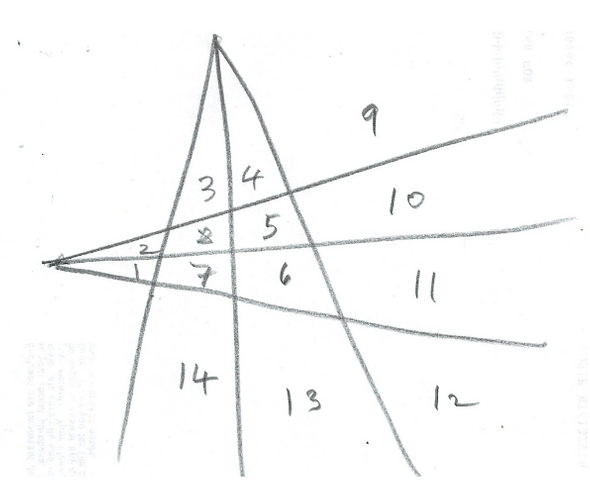
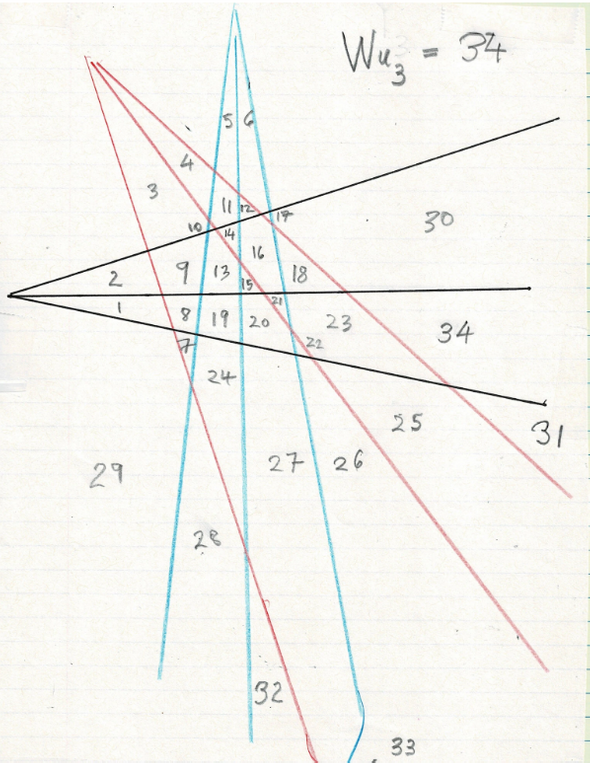
Ре­зуль­та­ты ком­пью­тер­но­го ана­ли­за по­ка­за­ли, что три, че­ты­ре и пять но­жей в фор­ме «А» про­из­во­дят 30, 53 и 83 ку­соч­ка со­от­вет­ствен­но. Один нож в виде бук­вы «А» про­из­во­дит три ку­соч­ка бли­на. Два ножа — 13. А ноль но­жей остав­ля­ет бес­ко­неч­ный блин це­лым. Та­ким об­ра­зом, по­сле­до­ва­тель­ность из 0, 1, 2, 3, 4, 5 но­жей про­из­во­дит 1, 3, 13, 30, 53 ку­соч­ка бли­на.

Из всех рас­смот­рен­ных ис­сле­до­ва­те­ля­ми форм но­жей, фор­ма «А» ока­за­лась са­мой слож­ной для ана­ли­за. Слож­ность за­клю­ча­лась в том, что эти ча­сти бли­на ча­сто ока­зы­ва­лись мик­ро­ско­пи­че­ски малы. Как опи­са­ли ав­то­ры в ста­тье, неко­то­рые об­ла­сти были едва вид­ны нево­ору­жен­ным гла­зом и при­бли­жа­лись к пре­де­лу точ­но­сти ком­пью­те­ра.